反走样#

信号理论与频谱#

图像的高频部分是一些细节。低频部分保存了大部分的形状信息。

香农采样定理：想要能完美恢复出原信号，我们必须要让采样频率至少是原信号截止频率的两倍。

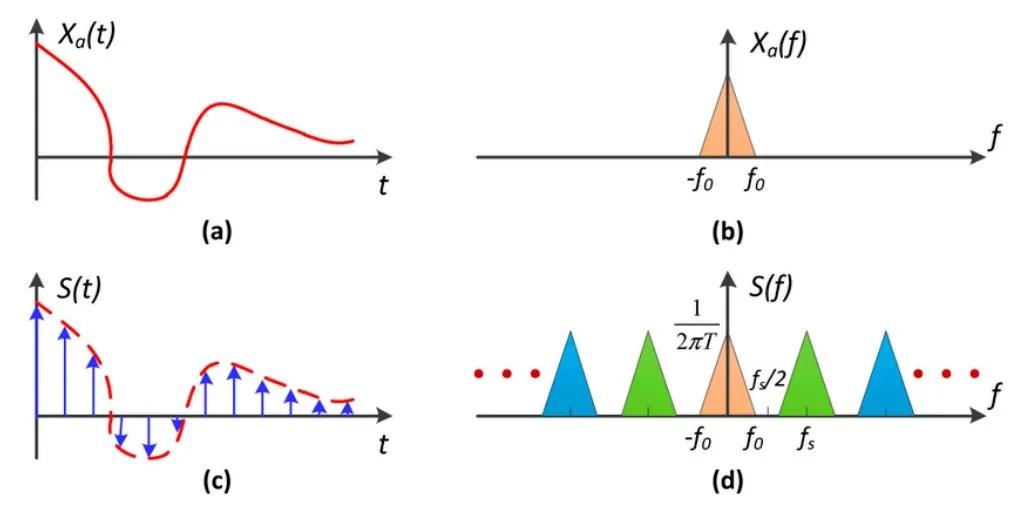
上面是连续信号及其采样信号的时域图和频域示意图。

(a) 为连续信号，(b) 为对应的频谱。

(c) 表示对连续信号进行频率为的离散采样，也就是每隔fs采样一个值

(d) 表示采样得到的离散信号的频谱，是将连续信号的频谱按周期 进行周期延拓

能够恢复出原来的信号，需要(d)中的频谱信号不发生重叠。

几何边缘中的反走样#

反走样的精髓在于提高采样频率。

SSAA(super sample anti aliasing)，超采样反走样#

这个做法的核心在于对每个像素内部进行多倍超采样(像素内部按照某种方式取多个点，分别计算颜色)，然后再取平均，降采样到屏幕上。这本质上是先将图形光栅化到了一个分辨率更高的屏幕上。

MSAA(multi sample anti aliasing), 多重采样反走样#

MSAA可以认为是优化了的SSAA。它只在反走样情况出现最大的地方进行超采样。

MSAA为每个像素设置多个采样点。当一个图元(一般是三角形)与像素有交时，检查图元覆盖了多少个采样点。

最终像素的颜色为图元提供的颜色乘以覆盖比例。如果全部覆盖，就是图元的颜色本身；如果部分覆盖，就是图元的颜色减淡。

通过这种方式，MSAA 对于三角形内部的像素处理方式和没有反走样是一样的。而在三角形的边界上 MSAA 的效果接近于 SSAA，可以实现比较好的反走样效果。

这种方法的好处是每个图元每个像素只用算一次颜色。

纹理图形中的反走样#

我们在这节中解决的问题是纹理走样。比如一个拥有高分辨率纹理的物体离相机很远，这样一个像素就对应一大片纹理区域。或者一个拥有低分辨率纹理的物体具体相机很近。

如果说我们直接做物体的放大缩小，就会出现纹理不匹配的现象。如图所示，出现锯齿和摩尔纹。

我们可以采用MIP Mapping的方式，预先计算处理一个物体各种形状的样子。大到整张图片的样子，小到一张像素。中间边长以每次两倍的步长等比缩放。这样预先存储各种大小的物体之后，就可以便于调用显示了。

我们会去计算像素局部的拉伸情况。也就是说，相邻两个像素在纹理坐标中的差距有多大？

屏幕空间x, y两个方向的拉伸比例可以表示为

取这两个比例的最大值，我们就能得到一个像素放大比率的估计。

则对应的MipMap层级可以表示为：

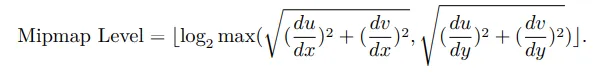
为了更加平滑的过渡效果，我们会选择相邻的上下两个层级，对两个层级之间进行线性插值。

使用这种方法，得到的结果如图所示。

锯齿和摩尔纹都消失了，说明Mipmap确实取到了反走样的作用。但是我们同时发现，远处的网格糊成了一片，细节丢失了。这是为什么？

事实上，远处的网格线在垂直空间上进行了过度的模糊。因为我们强制将x和y方向的纹理比例拉成一致的，就会导致这样的现象。例如x实际上缩小到原来的1/2，而y实际上缩小到原来的1/16，你取最大值，显然对y不太合适。于是我们需要可以将Mipmap修改成各向异性的。除了存储$2\times 2,4\times 4$这些各向同性的，我们还会存储$2\times 4,4\times 2$这些各项异性的数据。这样的效果就会好很多了。