物理模拟#
我们有公式F=ma,v′=a,x′=v.有了这三个公式,就可以模拟物理世界。
我们考虑的例子是在三维中的。所以其中的a,v,x都是三维向量,分别表示在x,y,z方向上的加速度,速度和位移。
离散化#
空间离散化#
我们认为空间是多个微元。将物体抽象为若干个质点,且有弹簧链接。
整个物体运动的模型就被抽象成了弹簧-质点模型。
对于一个连接质点i,j的弹簧,有:
fij=kij(∣∣xj−xi∣∣−lij)nij
其中fij是质点i受到弹簧的弹力,lij是弹簧原长,nij=∣∣xj−xi∣∣xj−xi是从i指向j的单位向量。
时间离散化#
我们认为时间是多个微元。每个微元中我们单独处理欧拉积分。这有显式、半隐式和隐式之分。
假设时间间隔为h。已知当前物体的状态(包括位置x和初速度v)时,可以计算出相应的受力情况。
设xk=(x1(tk),x2(tk)...xn(tk))T为时刻tk时各质点的位置构成的向量。它的形状是n×3的。
同理,设vk=(v1(tk),v2(tk)...vn(tk))T为时刻tk时各质点的速度构成的向量。它也是n×3的。
然后我们来处理力。我们上面说过,每个时间状态t,根据物体的位置x(t)信息,我们可以计算出受力情况。
我们假设对于时刻t,受力矩阵为f(t)=f(x(t)).注意这也是一个n×3的矩阵。
从受力矩阵到加速度矩阵,我们想要将每一行除以对应的质点质量。这相当于前乘一个质量倒数构成的对角矩阵。
令
M=m1⋮0⋯⋱⋯0⋮mn
M为质量构成的对角矩阵。则
M−1=m1−1⋮0⋯⋱⋯0⋮mn−1
那么我们的公式即为:
xk+1=xk+∫tktk+1v(t)dtvk+1=vk+∫tktk+1a(t)dta(t)=M−1f(x(t))
我们不想算积分,我们也算不出积分。于是我们最常用的假设就是积分中的值为定值。
视假设的定值不同,我们有下面三种近似计算积分的方式。
显式欧拉积分#
假设在时间区域(tk,tk+1)中,有
v(t)=v(tk)=vkx(t)=x(tk)=xk
那么,上式转化为:
xk+1=xk+hvkvk+1=vk+hM−1f(xk)
这就是一个马尔科夫链问题。每次由xk,vk就可以自动更新出xk+1,vk+1。
半隐式欧拉积分#
假设在时间区域(tk,tk+1)中,有
v(t)=v(tk+1)=vk+1x(t)=x(tk)=xk
那么,上式转化为:
xk+1=xk+hvk+1vk+1=vk+hM−1f(xk)
这其实也是一个马尔科夫链问题。每次由xk,vk,先更新出vk+1,再更新xk+1。
上面两种方法的问题在于它们不稳定**(为什么?如何定义不稳定性?如何严格证明它们的稳定性情况差异?如果你有见解欢迎联系笔者)**。
隐式欧拉积分#
隐式欧拉积分假设
v(t)=v(tk+1)=vk+1x(t)=x(tk+1)=xk+1
那么,上式转化为:
xk+1=xk+hvk+1vk+1=vk+hM−1f(xk+1)
这就不是简单地更新能搞定的事情了。这需要涉及到解方程。
求解隐式欧拉积分#
我们把v消掉。得到方程:
xk+1=xk+hvk+h2M−1f(xk+1)
然后,我们将这个方程转换成一个优化问题。我们假设f分为两个部分,其中一个部分为弹簧的弹力或说物体的内力fint=fint(x),与各质点的位置有关。另一个部分为外力fext=fext(t),只与时间t有关。于是,有方程:
xk+1=xk+hvk+h2M−1fext+h2M−1fint(xk+1)
令
yk=xk+hvk+h2M−1fext
则方程变为:
xk+1=yk+h2M−1fint(xk+1)
其中,fint是弹力,而弹力可以视为弹性势能的导数。即
fint(x)=−∂x∂E(x)
而到此,讲义上就非常不负责任地将它等价成了这样的形式:
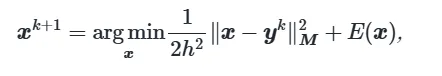
我们把这等式右边的这个函数记作g(x)。
注意,∣∣x−yk∣∣M2中,M是下标,它的意思是∣∣v∣∣M2=vTMv。
讲义上说:你可以通过计算目标函数g(x)关于x的梯度等于0证明等价性。
但是注意,g(x)关于x的梯度等于0只能说明解出来的xk+1是个极值点,不能说明为什么是最小值点。建立严格的等价关系,还需要加上g(x)严格凹这个条件,这等价于其黑塞矩阵正定。
我们下面补充一下关于等价性的证明。
关于上面方程等价于最小化g(x)的(不严谨)证明#
一方面,我们证明x为方程的解等价于x为g(x)的极值点。关于目标函数求梯度,得
∇g=2h212(x−yk)M−fint(x)
整理即可证。
另一方面,我们研究该函数的黑塞矩阵,证明其正定,以保证极值点的唯一性。
该函数的黑塞矩阵为
H=h21M+∇2(E)
我们认为在h足够小时,h21M是一个元素都足够大的正对角矩阵,它加上∇2(E),能够形成一个正定矩阵(因为最极端情况,是对角线为正且足够大,其余元素的影响忽略不计)。
这与我们的先验是一致的。我们知道切分的时间元必须得小,否则当然会出问题。
由于数学与物理方面的知识限制,我们暂时不能够详细地解出h的下界。但是在实验中一般能够探索出良好的h。
求解方程#
当方程转化为最小化目标函数之后,我们自然就可以通过梯度下降法或牛顿法等方法来处理之。