3D视觉#

3D视觉的任务是从图片中重建3D场景。这本质是一个从低维度到高维度的问题，照片上的一个点对应世界中的多个点(Single-view Ambiguity，单视图歧义)。解决这种问题的方法有光照投影，多目立体视觉等。

对极几何(Epipolar Geometry)#

对极几何是两张照片中形成的一些几何性质。

考虑两张照片，它们分别由在$O$和$O'$处的相机拍摄而成。如图所示。

设$OO'$交两张照片于$e,e'$。过$OO'$的连线任意作一个平面交两张照片于$l,l'$，这两条照片上的线成为极线。

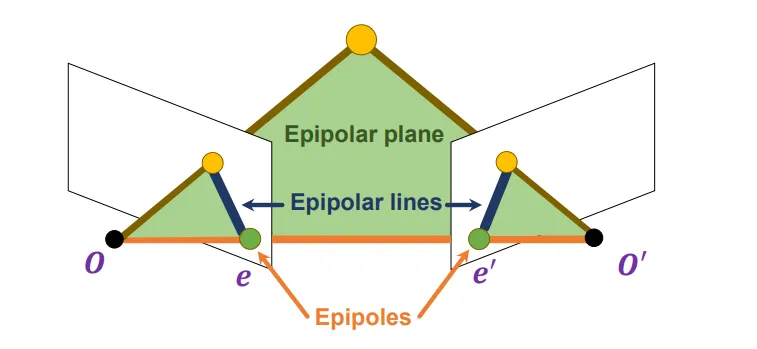
极线的性质：若点X在照片O上的投影点出现在$l$上，则X在O’上的投影点一定会出现在$l'$上。

这其实给了我们一种方式，在寻找对应点前，我们只需要在极线上寻找就可以了。

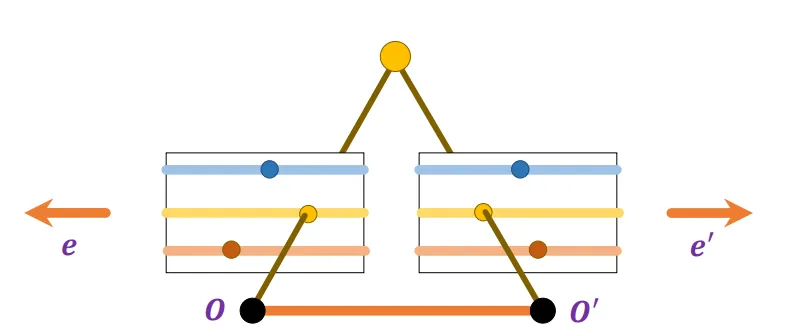
对极几何有一种特殊形式，即两张照片是平行的，且它们还平行于$OO'$的连线。这种情形下$e,e'$是无穷远点，极线就是过对应点作$OO'$的平行线。

Essential Matrix 与 Fundamental Matrix#

我们想要用数学形式描述好极线的限制。

我们建立世界系。还是两张照片，为了简单，世界系与O点的相机坐标系重合。于是对于世界系中齐次坐标点X就有：

$$x_{pixel} \cong K[I,0]X\\ x'_{pixel} \cong K'[R,t]X$$

我们定义：

$$x=K^{-1}x_{pixel} \cong [I,0]X\\ x'=K'^{-1}x'_{pixel} \cong [R,t]X$$

于是有：

$$x'\cong Rx+t$$

即$x',Rx,t$线性相关。这可以用这样的形式表示：

$$x'\cdot(t\times(Rx))=0$$

把$t_{\times}$写成一个矩阵，则有：

$$x'^T[t_{\times}]Rx=0$$

令$E=[t_{\times}]R$，则E称为Essential Matrix。有$x'^TEx=0$。

Essential Matrix描述了normalized image coordinates x与x’之间的关系。

如果我们想要直接地描述像素点之间的关系，我们可以把它们的表达式代入。得到：

$$x'_{pixel}(K'^{-1})^TEK^{-1}x_{pixel}=0$$

令$F=(K'^{-1})^TEK^{-1}$，即$x'_{pixel}Fx_{pixel}=0$。

下面我们来考虑E和F的自由度数。

$E=[t_{\times}]R$由旋转和平移方式唯一确定，且E还有缩放不变性。旋转和平移各有3个自由度，而缩放不变性减了一个自由度，故E的总自由度为5。

$F=(K'^{-1})^TEK^{-1}$，其秩为2，所以丢失了一个自由度，然后又由放缩不变性，所以F的总自由度为7。

计算F的方式还是和前面基本一样。将限制化成线性方程，然后采用最小特征值对应的特征向量的方式来求解F。

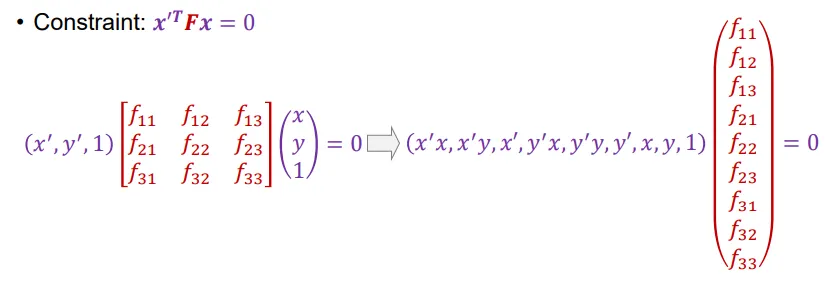
注意：这样求解出来的F不一定保证秩为2的限制。我们可以使用矩阵奇异值分解来进行处理。将解出来的F通过奇异值分解得到$F=U\Sigma V^T$，这里$\Sigma$是F的奇异值组成的对角矩阵。然后我们手动将最小的奇异值设置成0，就可以保证秩为2的限制。

在实际操作过程中，我们会发现系数矩阵中元素的大小差异很大。如果x,y的量级是$10^3$，那么系数就会有下面这样的量级。

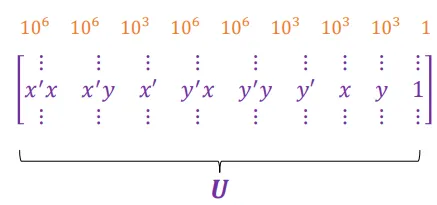
于是在实际操作中，我们会对相片坐标作坐标变换，将原点设置在所有匹配点的中心，缩放坐标使得原点到所有匹配点之间的平均距离为2。

双目立体视觉#

双目立体视觉的任务是从两张照片之中得到世界场景的深度图。像人的眼睛就是一个双目立体视觉的例子，眼睛看到的是两张图片，由大脑处理成为具有深度信息的3D世界。

从匹配点到深度图#

我们考虑一个简单的双目立体视觉的例子。在这个例子中，两张照片是平行的，两个相机之间只进行了一个x方向上的平移。如图所示。

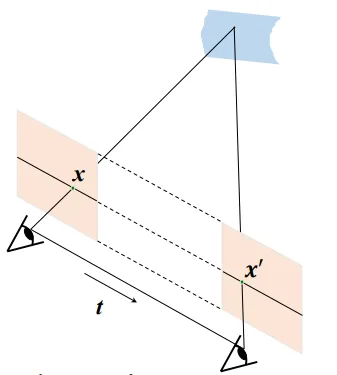
在这个例子中，y相同的线就是两张照片之中对应的极线。

我们的要做的事情是对于第一张照片中的每个点P，在第二张照片的极线上寻找对应的最佳匹配点P’。然后根据P与P’之间的距离，解出深度信息。如图所示，由相似可得：

$$\frac{OO'}{OO'-PP'}=\frac{z}{f}$$

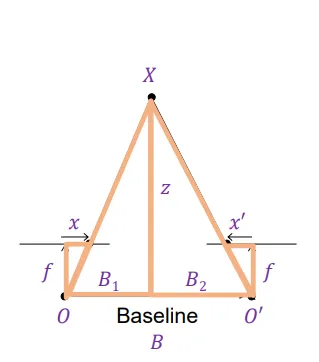
图中用x和x’来表示与相机系中的原点对应的x方向距离。由推导可知深度z与$x-x'$成反比，比例系数为$fB$。

寻找匹配点——暴力方法#

我们解决了找到匹配点后如何得到深度的问题。接下来我们来看看如何寻找匹配点。

最简单的方式是对于每个点考察对应极线上的所有点，一一比较(对于以点为中心的一个窗口，使用SSD距离什么之类的)并寻找最优匹配。这种方式低效，但是有效。有几个点需要注意：

1. 窗口大小如何选择？小的窗口会引入很多噪声，大的窗口会消灭很多细节信息。
2. 如果有些点在标准图片中存在，而在参考图片中对应的点不存在(如被遮挡)怎么办？会导致不匹配。
3. 如果图片中有重复的相同纹样，则会很容易导致误匹配。

寻找匹配点——基于动态规划的全局优化方法#

我们引入三个不一定正确的假设。

1. 一张图片中的一个点在另一张图片中最多有一个匹配点。
2. 匹配点在极线上都是按照顺序分布的。
3. 两张图片的匹配点之间的距离不会太大。

这样的话，我们就可以将匹配问题转换成一个动态规划问题。我们寻找两条相互对应的极线，将上面的点按顺序排列，假设都是0到N。对于每两个点之间的匹配，我们定义一个匹配代价函数$Cost(i,j)$。如果单个点出现不匹配，则我们认为代价为一个常数值C。

我们需要找到一种匹配方式最小化总匹配代价。

记$dp[i][j]$为：对于第一条极线上的0-i与第二条极线上的0-j点进行匹配的最小代价。

则可以写出状态转移方程：

$$dp[i][j]=max(dp[i-1][j-1] + Cost(i,j) , dp[i-1][j] + C , dp[i][j-1] + C)$$

得到最终的$dp[N][N]$，并回溯即可。

如果我们认为两张图片的匹配点之间的距离不会太大，那么我们就只需要对$|i-j|<M$的$i,j$进行计算了。

Structure from Motion#

**Structure from Motion的输入是许多从不同相机拍摄而来的图片，输出一方面是是相机参数，一方面是3D结构。**为了简单，我们考虑对仿射相机作SFM问题。

仿射相机#

仿射相机是对一般相机的一种简单化。记得我们在相机投影矩阵的推导中说到，相机坐标的$(x,y,z)$被映射为相片坐标中的$(f\frac{x}{z},f\frac{y}{z})$，然后再去进行平移和旋转。所谓仿射相机，就是我们认为在图片中是直接把z丢弃，然后再在相机坐标系中进行一组线性变换。

对于仿射相机而言，相机矩阵P的形式如下：

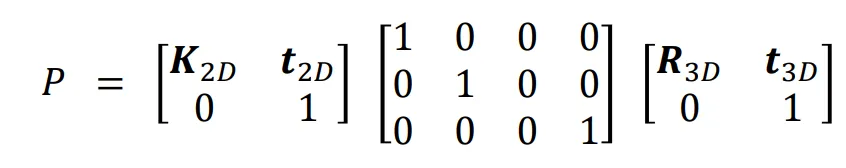
其中最右边的一个矩阵表示在三维空间中的旋转与平移；中间的矩阵表示丢弃z坐标的投影矩阵；左边的矩阵表示在二维空间中的缩放与平移变换。

其中$K_{2D}=\begin{bmatrix}s & 0\\0 & s\end{bmatrix}$表示一个缩放变换。$t_{2D}$表示一个平移变换。

可以把P写成下面的形式：

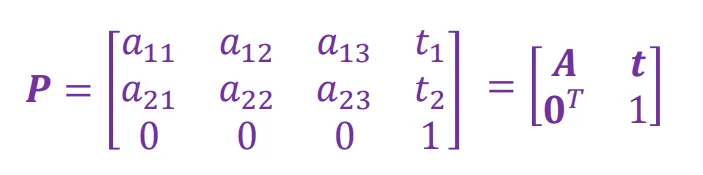
在非齐次坐标下：

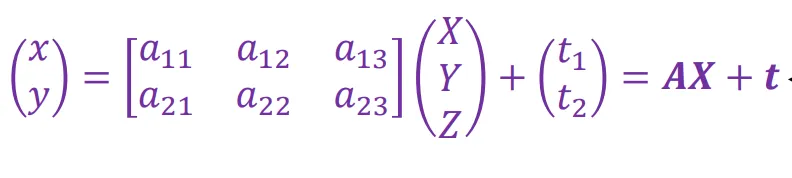
仿射相机的SFM求解#

暂时先忽略可见性的问题。我们把问题建模成n个相同的3D点出现在m张图片中，即方程组：

$$x_{ij}\cong P_iX_j(i = 1,2,...m; j = 1,2,...n)$$

你会发现，对于可逆矩阵$Q_{4\times 4}=\begin{bmatrix} Q & T \\ 0 & 1\\ \end{bmatrix}$,如果我们让所有的$P_i$变成$P_iQ$，让$X_j$变成$Q^{-1}X_j$，方程依然是成立的。

方程数目为2mn个：每个$x_{ij}$的x,y坐标各提供一个方程。

变量数为$3n+8m$个。每个3D点贡献3个变量，每个相机的P矩阵贡献8个变量。

因为Q的任意性，所以将问题的自由度减少了12。总之，我们需要$2mn\ge8m+3n-12$，这样的方程组才能有某种程度上的唯一解。

接下来我们来求解这个方程组。

首先我们将问题转成非齐次坐标的形式。即

$$x_{ij}=A_iX_j+t_i$$

然后，我们定义

$$\hat{X}_i=X_i-\frac{1}{n}\Sigma X_k\\ \hat{x}_{ij}=x_{ij}-\frac{1}{n}\Sigma x_{ik}=A_i(X_j-\frac{1}{n}\Sigma X_k)=A_i\hat{X}_j$$

这相当于是把x和X均进行了归一化操作。然后我们的方程就变成了比较美丽的形式：

$$\hat{x}_{ij}=A_i\hat{X}_j$$

这样，我们可以把所有的方程统一写成一种矩阵乘的形式：

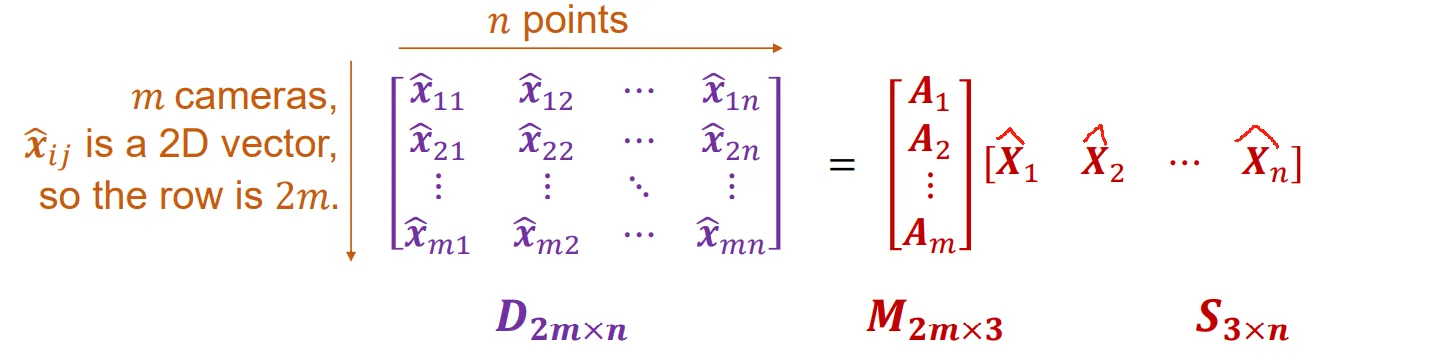
现在是给定D，要求M和S。这个问题可以通过奇异值分解来解决。设D的奇异值分解结果为$D=U\Sigma V^T$，由于噪音等因素，$\sum$可能不止有三个非零元，但是我们只保留D的前三大的奇异值。得到：$D\approx U\Sigma_{3\times3}V^T$。

这就基本上解出了M和S。但是有个小问题是$\Sigma$矩阵如何分派到两边。其实这里可以任意让。这其实对应了上面所说的Q的任意性。在实际中，论文提出令$M=U\Sigma^{\frac{1}{2}},S=\Sigma^{\frac{1}{2}}V^T$。

解出$\hat{X}$之后怎么回到原来的X呢？这其实也有个小问题，在PPT中并没有涉及。其实如果你让所有的$X_j$变成$X_j-\alpha$，$t_i$变成$t_i+A_i\alpha$，原方程也是依然成立的……

所以可以不妨设$X_i$的中心就是0，即$X_i=\hat{X}_i$。

接下来我们来消除歧义性。

使用的条件是：$A_i=\begin{bmatrix}a_1\\a_2\end{bmatrix}$矩阵应该是单位正交的(在相机参数中进行展开可得)。即$||a_1||=||a_2||=1$，$a_1\cdot a_2=0$。

我们需要找到矩阵$Q_{3\times3}$，让所有的$A_i$变成$A_iQ$，让$X_j$变成$Q^{-1}X_j$，然后使得

$$(A_iQ)(A_iQ)^T=I_{2\times 2}$$

令$N=QQ^T$，用方程组$A_iNA_i^T=I$解出N，然后进行Cholesky分解，把N分解成$QQ^T$。这样就能找到对应的Q。

数据信息的使用方式——Incremental Structure from Motion#

我们到目前为止都是假设所有点在所有相片中都可见。但是在实际问题中这显然不现实。于是我们使用增量SFM的方式动态处理这些数据。

基本的思想是先找n个点和m张照片，使得n个点在m张照片中都有出现。如上所示解出n个点的世界坐标和m张照片的相机参数。然后每次可以加入一张新照片或加入一个新点。

• 加入一个照片要求这张照片中至少出现了3个已知的世界点。可以通过解方程来解出相机的参数。
• 加入一个世界点要求这个点至少在2张已知的照片中出现了。可以通过三角化来解出这个点的坐标。

实际操作中，每次会挑选具有最多匹配点的照片，在所有匹配点上运行RANSAC方法来计算相机参数，然后查找这张照片和别的照片进行匹配，看有没有匹配出新的特征点。如果有，就使用三角化计算出新的特征点的坐标。

多目立体视觉#

多目立体视觉是双目立体视觉的自然延伸。它的输入是一个物体的多张相片，相片对应的相机参数都是已知的。与SFM只考虑特定匹配点的做法不同，多目立体视觉重建的是整个物体。

多目立体视觉问题有许多种解决方式。我们主要来介绍基于Patch的做法。

什么是Patch#

Patch是真实世界中的一些物体表面块。如图所示。这和用多边形网格表示物体的做法有相似性。

数学上描述一个Patch，可以用这些参数：

• 中心位置$c(p)=(x,y,z)$
• 法线向量$n(p)=(n_x,n_y,n_z)$
• 范围大小，用半径$r$表示。一般我们设置范围大小使得Patch在照片中对应大约9*9像素区域。

定量描述匹配度与patch的好坏#

我们的任务是基于给定的照片来重建Patch。首先我们来量化Patch在两张照片中的匹配程度。给定一个Patch $p$，两张照片$I,J$。我们会在Patch上选若干个代表点$P_1,P_2...P_n$，计算出这些代表点在两张照片上的投影分别为$I_k,J_k$。则定义这两张照片对于Patch $p$的匹配程度：

$$N(I,J,p)=\frac{\Sigma(I_k-\bar{I})(J_k-\bar{J})}{\sqrt{\Sigma(I_k-\bar{I})^2\Sigma(J_k-\bar{J})^2}}$$

熟悉的同学可以看出这是相关系数的形式。为什么计算相关系数而不是像SSD之类的函数？因为不同照片之间可能会因为光照等因素导致颜色并不完全一致。但是颜色的对比度(即比例)应该是一致的。所以这里计算相关系数会更为合理。

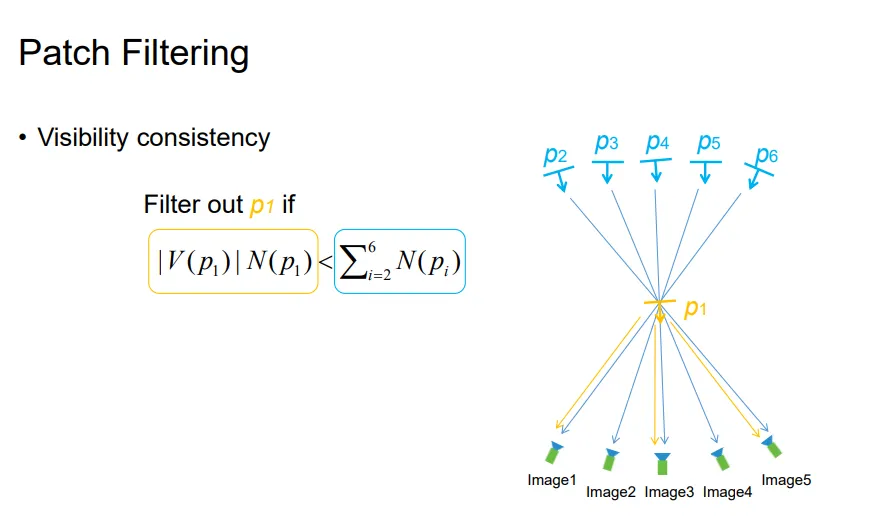
那么我们就可以进一步地定义选择的一个Patch $p$的好坏程度。定义$V(p)$为所有可见到p的照片。则p的评估函数：

$$\displaystyle N(p)=\frac{1}{(n+1)n/2}\sum_{i<j,\in V(p)}N(I_i,I_j,P)$$

于是对于固定的V(p)，patch就变得可评估，于是便可优化了。优化的参数无非就是中心和法向量。

但是$V(p)$也需要更新。下面我们来看看$V(p)$更新的步骤。初始令V(p)为所有图片，然后两两计算N值。

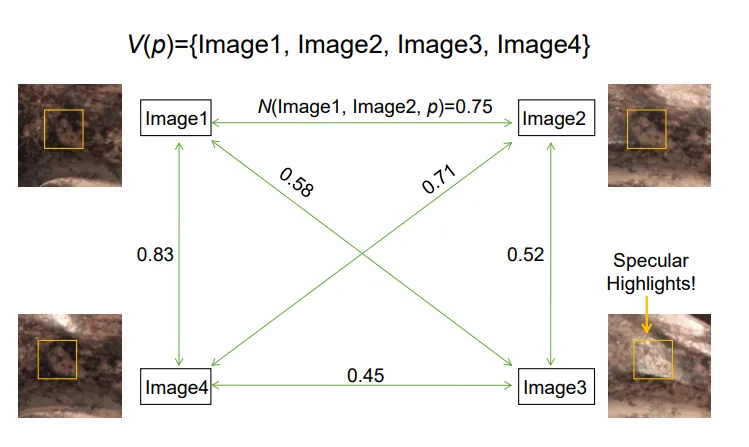
然后保留N值和最大的图片作为参考图片。例如Image1的N值和为$0.75+0.58+0.83$。

以参考图片为中心，选取N值大小不小于某一个Threshold的边以进行保留。如图，如果选取Threshold为0.7，则可以保留图片1，2和4。舍弃图片3。如果最终剩余的图片数目不低于某个值，我们就接受这个Patch。

到目前为止，我们先总结一下Patch based MVS的算法过程：

1. 每张图片Feature detection，然后两两图片之间作Feature matching。得到若干Matching点对，对这些Matching点对，使用三角化计算出世界坐标。
2. 对于每个1中计算出来的世界坐标点，构建以它为中心的Patch p，法向方向随机选择(一般会选指向Match出它的两张照片之一，或者指向平分方向)，然后通过上面所说的V(p)更新的方式，找到合适的一个V(p)集合。如果最终剩余的图片数目不低于某个值，我们就接受这个Patch。
3. 如果接受了这个patch，则对于这个V(p)集合，优化patch参数以最大化N(p)。

Patch Expansion与Patch Filtering#

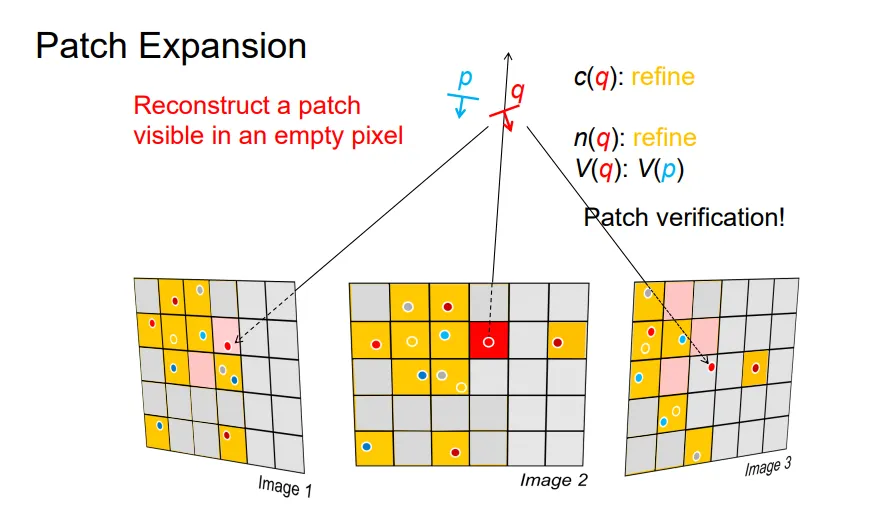
依照上面的算法构建出的Patch还是稀疏的，它总是要依赖于图像匹配。基于Patch的MVS最好的一个特性就是patch可以拓展。

基于上面的算法走完之后，我们会对每张图片的每个像素，记录一下它是否被Patch占据了。如果它被占据且周围有邻居(下图中红色的格)，我们会自然而然地认为图中红色区域内很容易能够出现潜在的匹配现象。

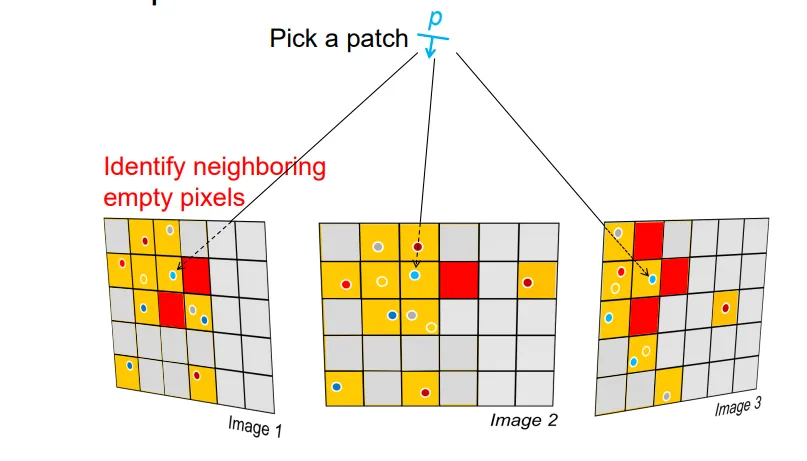
基于此我们会选择一个红格，基于它去构建一条线，在这条线上优化一个合适的Patch。然后查看这个Patch能不能成为好的Patch。

此外，我们还会对一些不好的Patch进行删除。具体细节不再展开了。

基于光照强度的表面重建(Photometric Stereo)#

另一种表面重建的方式是基于光照强度的表面重建。不同法向的物体表面，在相同光照条件下会呈现不同的亮度。我们利用这一点，从多种光照强度下摄像，可以重建物体的表面法向，进一步，将物体表面呈现出来。

这种算法的输入是同一物体在不同光照条件下的照片，输出是物体的表面信息。

从光照强度到法向量#

根据缩放不变性，我们把法向量$(n_x,n_y,n_z)$描述成$(p,q,1)$。

物体的表面点在光照条件下呈现出来的亮度$I$由下面几项决定：

• 物体的材质。
• 光照条件。
• 物体表面的法向量。

我们假设光照条件和物体材质保持不变，那么$I$就是法向量的函数。可以描述成$I=R(p,q)$。

这个R函数与反射模型有关。如果是完全漫反射的话，R就是一个定值(在这种条件下，我们没有办法基于光照强度求解法向量……)

对于Blinn-Phong 反射模型$I=\rho(n\cdot s)$，其中s是半程向量，在给定光源和视角条件下是已知值，我们也把它描述成$(p_s,q_s,1)$的形式。

我们会有：

$$I=R(p,q)=\frac{p_sp+q_sq+1}{\sqrt{p_s^2+q_s^2+1}\sqrt{p^2+q^2+1}}$$

固定一个$I$，在$(p,q)$平面上，这样一条曲线是圆锥曲线。

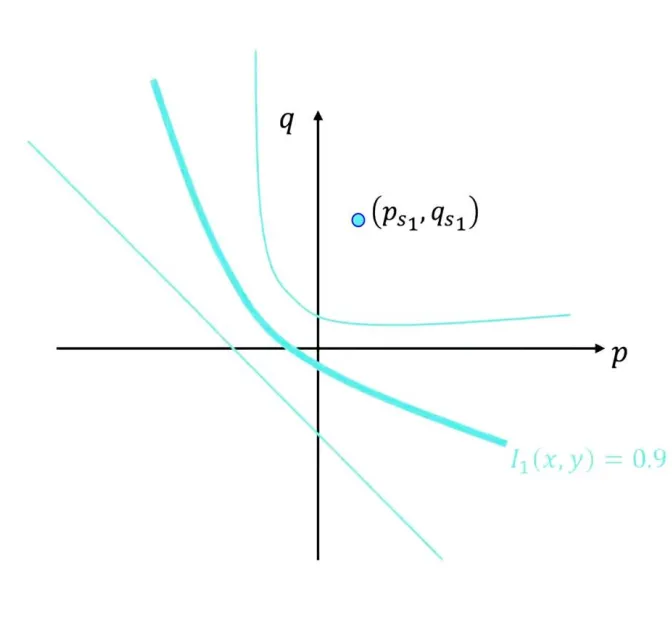
我们需要几条这样的圆锥曲线才能唯一确定一个点的法向？两条圆锥曲线一般有多于一个交点，于是三条圆锥曲线(即三张照片信息)能够唯一确定一个法向方向。

接下来，我们使用线性方程的形式来解这个问题。我们有三个方程：

$$I_k=\rho s_k\cdot N$$

写成矩阵乘法的形式：

$$\begin{bmatrix} I_1 \\I_2\\I_3 \end{bmatrix} = \rho \begin{bmatrix} s_{x1} &&s_{y1}&&s_{z1}\\ s_{x2} &&s_{y2}&&s_{z2}\\ s_{x3} &&s_{y3}&&s_{z3} \end{bmatrix} N$$

有$\rho N=S^{-1}I$。可把$\rho N$归一化得到法向形式。

如果需要屏蔽噪声影响，得到更精确的N，可以引入更多照片，从而转化成解超定方程组。

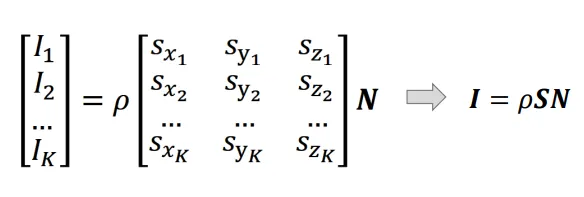
这就是解非其次超定方程$AX=B$，我们一般使用最小二乘的设计方法，来最小化$||AX-B||^2$。展开并进行求导，这个方程的解形式应该是$X=(A^TA)^{-1}A^TB$。

到目前，我们总结一下。我们会在同一视角但是不同光照条件下，对一个物体拍摄多张照片。由这多张照片中每个点的光照强度信息，我们可以解出每个点的法向量信息。如图所示：

从法向量到表面重建#